Question

Find n. (n!)²- 4n! - 12 = 0​

Answer 1

n=6 , n=-2

Explanation:

`n^(2)-4n-12=0`

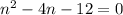
Factorise to give:

`(n-6)(n+2)`

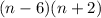
Set first one to equal 0:

`n-6=0`

`n=6`

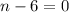
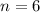
Set second one to equal 0:

`n+2=0`

`n=-2`

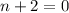
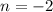
Reason for 2 solutions:

All quadratics can have a maximum of 2 solutions like this one or a minimum of 0.

The solution(s) is the point where the graph crosses the x-axis

The image below shows the graph of the equation:

`n^(2)-4n-12`

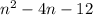
When y=0:

It intercepts the x-axis at 6 and -2 giving why n has 2 solutions