Answer: 3/2
======================================================
Step-by-step explanation:
PDF = probability density function
The given joint PDF is
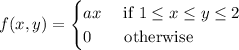
Let's focus on the
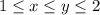 . Specifically the x term for now. Erasing out the y term, we have the inequality
. Specifically the x term for now. Erasing out the y term, we have the inequality
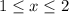 which says x is between 1 and 2, inclusive. We have almost the same story for y, but there's another condition attached to it: y must also be equal to or larger than x.
which says x is between 1 and 2, inclusive. We have almost the same story for y, but there's another condition attached to it: y must also be equal to or larger than x.
So let's say x = 1.5. This would mean
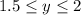 . As another example, x = 1.7 leads to
. As another example, x = 1.7 leads to
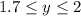 . In general, we would say
. In general, we would say
 where x is between 1 and 2.
where x is between 1 and 2.
As x gets bigger, the range of possible y values gets smaller. If x = 2, then y has no choice but to be 2 as well.
-----------------
Based on that, we'll have a double integral that looks like this:
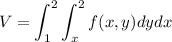
The outer integral handles the x terms that range from 1 to 2, describing
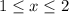 . Note the dx on the outside. The order of the dy and dx matters.
. Note the dx on the outside. The order of the dy and dx matters.
On the inside, we have the integral for dy ranging from x to 2 to describe the interval

To have f(x,y) be a PDF, the volume under the f(x,y) surface must be 1, where the volume is based on the bounds set up. So we must have V = 1. We'll use this later.
-----------------
Let's simplify the double integral.
We'll start by computing the inner integral with respect to y.
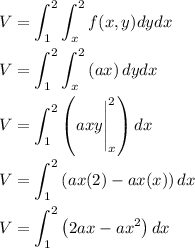
Then we'll finish it off by integrating with respect to x.
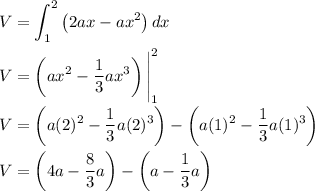
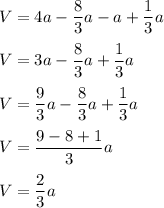
Side note: We don't have to worry about the "plus C" integration constant when working with definite integrals.
Recall that V = 1. So,
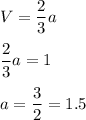
a = 3/2 is the final answer.