Answer:
Speed of waves on the rope is 21 m/s
Step-by-step explanation:
Length of the rope (l) = 5.0 m
Mass of the rope (m) = 0.52 kg
Tension in the rope (T) = 46 N
Formula of speed of waves on the rope:
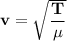
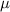 = Mass per unit length of the rope (m/l)
= Mass per unit length of the rope (m/l)
By substituting the values in the formula we get:
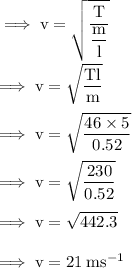
Speed of waves on the rope (v) = 21 m/s