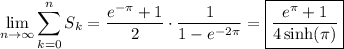Question

Given the curve
`\displaystyle \large{y=e^(-x)\sin x \ \ (x\geq 0)` let the area enclosed by the curve and the x-axis (above the x-axis) be S0, S1, S2, ... , Sn, ... in order from y-axis. Find
`\displaystyle \large{ \lim_(n \to \infty) \sum_(k=0)^(n) S_k}`

Answer 1

The given curve crosses the x-axis whenever x is a multiple of π, and it lies above the x-axis between consecutive even and odd multiples of π. So the regions with area S₀, S₁, S₂, ... are the sets

`R_0 = \left\{(x, y) : 0 \le x \le \pi \text{ and } 0 \le y \le e^(-x)\sin(x)\right\}`

`R_1 = \left\{(x, y) : 2\pi \le x \le 3\pi \text{ and } 0 \le y \le e^(-x)\sin(x)\right\}`

`R_2 = \left\{(x, y) : 4\pi \le x \le 5\pi \text{ and } 0 \le y \le e^(-x)\sin(x)\right\}`

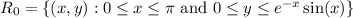
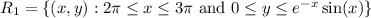
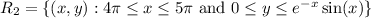
and so on, with

`R_k = \left\{(x, y) : 2k\pi \le x \le (2k+1)\pi \text{ and } 0 \le y \le e^(-x)\sin(x)\right\}`

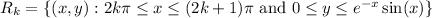
for natural number k.

The areas themselves are then given by the integral

`S_k = \displaystyle \int_(2k\pi)^((2k+1)\pi) \int_0^{e^(-x)\sin(x)} dy \, dx = \int_(2k\pi)^((2k+1)\pi) e^(-x)\sin(x) \, dx`

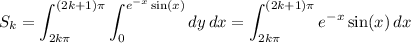
Integrate by parts twice. Take

`u = e^(-x) \implies du = -e^(-x) \, dx`

`dv = \sin(x) \, dx \implies v = -\cos(x)`

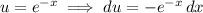
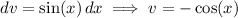
so that

`\displaystyle \int e^(-x)\sin(x) \, dx = -e^(-x)\cos(x) - \int e^(-x)\cos(x) \, dx`

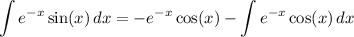
then

`u = e^(-x) \implies du = -e^(-x) \, dx`

`dv = \cos(x) \, dx \implies v = \sin(x)`

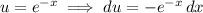
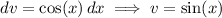
so that

`\displaystyle \int e^(-x)\cos(x) \, dx = e^(-x)\sin(x) + \int e^(-x)\sin(x) \, dx`

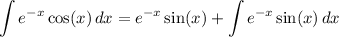
Overall, we find

`\displaystyle \int e^(-x)\sin(x) \, dx = -e^(-x)\cos(x) - e^(-x)\sin(x) - \int e^(-x)\sin(x) \, dx`

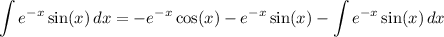
or

`\displaystyle \int e^(-x)\sin(x) \, dx = -\frac12 e^(-x) (\cos(x)+\sin(x)) + C`

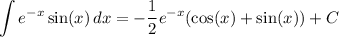
Using the antiderivative and the fundamental theorem of calculus, we compute the k-th area to be

`\displaystyle S_k = -\frac12 e^(-(2k+1)\pi) (\cos((2k+1)\pi)+\sin((2k+1)\pi)) + \frac12 e^(-2k\pi) (\cos(2k\pi)+\sin(2k\pi))`

`\displaystyle S_k = \frac12 e^(-2k\pi) \cos(2k\pi) \left(e^(-\pi) + 1\right)`

`\displaystyle S_k = \frac{e^(-\pi)+1}2 e^(-2k\pi)`

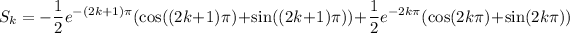
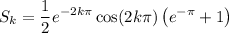
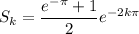
Since
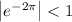`\left|e^(-2\pi)\right|<1`, the sum we want is a convergent geometric sum. As n goes to ∞, we have

`\displaystyle \lim_(n\to\infty) \sum_(k=0)^n S_k = \frac{e^(-\pi)+1}2 \cdot \frac1{1 - e^(-2\pi)} = \boxed{(e^\pi+1)/(4\sinh(\pi))}`