Question

Find an equation in slope-intercept form of the line satisfying the specified conditions.

Through (8,-3), perpendicular to -6x + 7y=-62.

Answer 1

`y = - (7)/(6) x + 6 (1)/(3)`

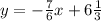
Explanation:

Slope-intercept form

y= mx +c, where m is the slope and c is the y-intercept.

-6x +7y= -62

Rewriting this equation into the slope-intercept form:

7y= 6x -62

`y = (6)/(7) x - (62)/(7)`

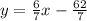
The product of the slope of 2 perpendicular lines is -1.

Let the slope of the unknown line be m.

`m( (6)/(7) ) = - 1`

`m = - 1 / (6)/(7)`

`m = - (7)/(6)`

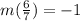
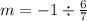
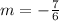
Substitute the value of m into the equation:

`y = - (7)/(6) x + c`

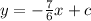
To find the value of c, substitute a pair of coordinates into the equation.

When x= 8, y= -3,

`- 3 = - ( 7)/(6) (8) + c`

`- 3 = - (28)/(3) + c`

`c = (28)/(3) - 3`

`c = (19)/(3)`

`c = 6 (1)/(3)`

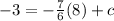
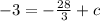
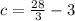
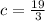
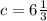
Thus, the equation of the line is
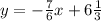`y = - (7)/(6) x + 6 (1)/(3)`.