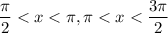Question

What is the solution to the trigonometric inequality sin(x)>1+cos(X) over the interval 0<=x<=2pi radians?

Answer 1

Last choice

Explanation:

First, convert (sinx)^2 to 1-(cosx)^2 via trigonometric identity derived from (sinx)^2 + (cosx)^2 = 1

`\displaystyle \large{\sin^2x + \cos^2x=1 \longrightarrow \sin^2x=1-\cos^2x}`

Thus, the rewritten inequality is
`\displaystyle \large{1-\cos^2x>1+\cos x}`

Notice how the inequality has a quadratic pattern since we have (cosx)^2 and cosx in the inequality, simply arrange degrees in order.

`\displaystyle \large{1-\cos^2x>1+\cos x}\\\displaystyle \large{0>1+\cos x-1+\cos^2x}\\\displaystyle \large{0>\cos x+\cos^2x}\\\displaystyle \large{\cos^2x+\cos x < 0}`

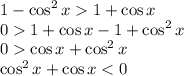
Then we factor cosx since the expression has cosx as a common factor.

`\displaystyle \large{\cos x(\cos x+1)<0}`

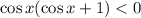
Then we have to consider each inequalities which are cosx<0 and cosx+1<0 then merge both intervals once obtaining the solutions.

(1)
`\displaystyle \large{\cos x < 0}`

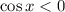
This inequality means that we have to find the x-value(s) that satisfy(ies) it.

Since cosx becomes negative after π/2 (Refer to unit circle, cosx becomes negative in second quadrant and this quadrant), that means it becomes negative until it reaches or < 3π/2.

Thus,
`\displaystyle \large{(\pi)/(2)<x<(3\pi)/(2)}` is the solution to cosx > 0.

The another way to solve inequality is to find the intersections by solving the equation then joint the interval together.

`\displaystyle \large{\cos x<0 \longrightarrow \cos x=0}`

From the unit circle, cosx becomes 0 at x = π/2 and x = 3π/2 between interval [0,2π]

Therefore:

`\displaystyle \large{\cos x = 0 \longrightarrow x = (\pi)/(2), (3\pi)/(2)}\\\displaystyle \large{\boxed{(\pi)/(2)<x<(3\pi)/(2)}}`

(2)
`\displaystyle \large{\cos x+1<0 \longrightarrow \cos x <-1`

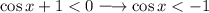
For this inequality, it appears that there have no solutions because cosine function is defined between [-1,1] in range hence there are no x-values in real plane that make cosx even less than -1.

Because only π satisfies cosx = -1 but not cosx < -1, we restrict π and every values.

Hence no solutions which cause a break of interval between π and π/2 < x < 3π/2

If you substitute x = π in, the inequality is false and therefore the answer is:

`\displaystyle \large{(\pi)/(2)<x<\pi, \pi<x<(3\pi)/(2)}`