Answer:
A: geometric; 4 times
B: arithmetic: 4 more
Explanation:
An arithmetic model is a linear model, where the rate of change is constant. Growth or decay is by a constant amount from one interval to the next.
A geometric model is an exponential model, in which the rate of change is proportional to the amount. Growth or decay is by a constant factor from one interval to the next.
__
A)
The equation for the sequence is given in "explicit" form:
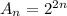
The exponent can be split so this can be rewritten as ...

If this were written in recursive form, it would look like ...
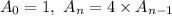
The fact that terms are related by a constant factor tells you the model is geometric. The factor tells you each hour the population is 4 times what it was in the previous hour.
__
B)
The given equation is in "recursive" form. It tells you each term is 4 more than the previous one. This constant difference between terms means the model is arithmetic.
_____
Additional comment
In general, words like "more" or "increase" refer to addition, and the words "times" or "factor" refer to multiplication.