Answer:
About 317 bacteria.
Explanation:
We can use the model for exponential growth:
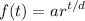
Where t is the time (in hours) that has passed and d is the time in which one "cycle" occurs.
Since the initial population is 50 bacteria, a = 50:
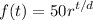
The population doubles every 15 hours. Hence, r = 2 and d = 15:

Therefore, the population after 40 hours will be:
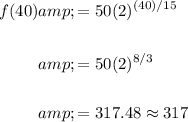
In conclusion, the population of the bacteria after 40 hours will be about 317 bacteria.