- Mass of the toy (m) = 12 Kg
- Acceleration due to gravity (g) = 9.8 m/s^2
- Height (h) = 5 m
- Initial velocity (u) = 0
- Let the final velocity be v.
- We know, for a freely falling body,
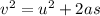
- Putting the values in the above equation, we get
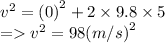
- Let the kinetic energy of the toy just before it hits the ground be K.E.
- We know,
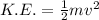
- Putting the values, we get
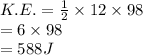
Answer:
The kinetic energy of the toy just before the toy hits the ground will be 588 J.
Hope you could get an idea from here.
Doubt clarification - use comment section.