Question

Given the function f'(x) = x3 + 12x2 + 36x, determine all intervals on which f' is increasing

Answer 1

`(-\infty,\, -6)` and
`(-2,\, \infty)`.

Explanation:

A continuous function is increasing if and only if its first derivative is positive.

Differentiate
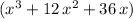`(x^(3) + 12\, x^(2) + 36\, x)` with respect to
`x` to find the first derivative of this function.

`\begin{aligned}& (d)/(d x) \left[x^(3) + 12\, x^(2) + 36\, x\right] \\ =\; & 3\, x^(2) + 24\, x + 36 \\ =\; & 3\, (x^(2) + 8\, x + 12)\end{aligned}`.

In other words, the given function is increasing if and only if
`3\, (x^(2) + 8\, x + 12) > 0`.

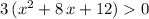Notice that
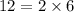`12 = 2 * 6` while
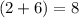`(2 + 6) = 8`. Thus, the quadratic expression
`3\, (x^(2) + 8\, x + 12)` may be rewritten as:

`\begin{aligned} & 3\, (x^(2) + 8\, x + 12) \\ =\; & 3\, (x + 2) \, (x + 6)\end{aligned}`.

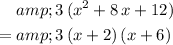Thus, the requirement that
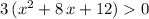`3\, (x^(2) + 8\, x + 12) > 0` is equivalent to
`3\, (x + 2) \, (x + 6) > 0`, which is true if and only if:

• either
  `(x + 2) < 0` and
  `(x + 6) < 0`, or
• 
  `(x + 2) > 0` and
  `(x + 6) > 0`.

Equivalently,
`3\, (x + 2) \, (x + 6) > 0` is true if and only if:

• 
  `x < (-2)` and
  `x < (-6)`, or
• 
  `x > (-2)` and
  `x > (-6)`.

The first requirement simplifies to
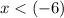`x < (-6)` and corresponds to the interval
`(-\infty, \, -6)`.

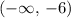The second requirement simplifies to
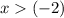`x > (-2)`, which corresponds to the interval
`(-2,\, \infty)`.

Thus, the given function is increasing on the interval
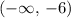`(-\infty, \, -6)` and
`(-2,\, \infty)`.