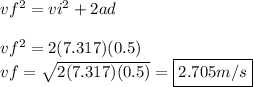Hi there!
We can begin by identifying the moment of inertia for the objects that will rotate.
For both a uniform cylinder and disk, the moment of inertia is equivalent to:
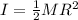
Let:
T₁ = Tension of rope section connecting rolling cylinder to pulley
T₂ = Tension of rope section connecting hanging mass to pulley
m₁ = mass of cylinder
m₂ = mass of pulley
m₃ = mass of hanging block
a = acceleration of entire system
g = acceleration due to gravity
We can begin by doing a summation of torques about the pulley:
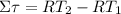
Rewrite using the rotational equivalent of Newton's Second Law:
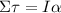
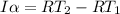
Rewrite alpha as a/r and substitute in the moment of inertia:
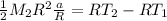
Cancel out the radii:
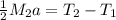
Now, we must solve for each tension.
T₁
Sum torques acting on mass 1 and use the same method as above:
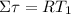
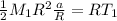
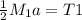
T₂
We can use a summation of forces:
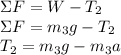
Plug these derived expressions into the above:
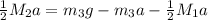
Rearrange to solve for acceleration:
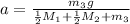
Solve for a:
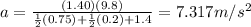
Now, we can use the following kinematic equation to solve for velocity given acceleration and distance: