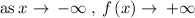Answer: See below
Explanation:
![\begin{array}{l}f\left(x\right)=3√(-x+2\ )\\\\Domain:\ \text{Case 1:}\ √(-x+2\ )\\\\\ x\ +\ 2\ \ge\ 0\ \\=-x\ \ge-2\\=\ x\ \le2\\\\\text{Case 2}:\ -x\ +\ 2\ \longrightarrow\ x\in\mathbb{R}\\\\\therefore\left(-\infty,\ 2\right]\end{array}](https://img.qammunity.org/2022/formulas/mathematics/high-school/4faa4sri94b1l9momt0r2hz1rsmd5e3dnl.png)
You can use Desmos so no need for complicated math
HA = None
VA = None
x-intercept = 2 - (2, 0)
y-intercept (exact value, Desmos only gives decimals)
f(0)=3√2-(0)
f(0)=3√2 <-- y-intercept (0, 3√2)
End behavior: Graph of f(x) moving to the left, but slowly going upwards, x-values decreasing but y-values increasing so