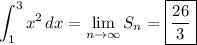Split up the interval [1, 3] into n equally spaced subintervals. Each one has length (3 - 1)/n = 2/n, so we're talking about the partition
[1, 1 + 2/n] U [1 + 2/n, 1 + 4/n] U [1 + 4/n, 1 + 6/n] U … U [1 + 2 (n - 1)/n, 3]
Let f(x) = x². Consider the left endpoints of each subinterval, given by the sequence x(i) = 1 + 2 (i - 1)/n for 1 ≤ i ≤ n. Then the area under the graph of f(x) over [1, 3] is approximated by the Riemann sum,
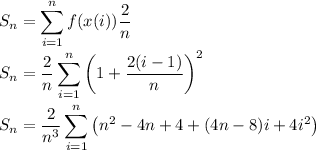
To compute the sum, recall the formulas,

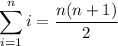
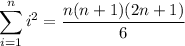
Then
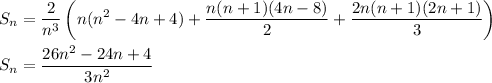
and the exact area under the curve over [1, 3] is