Answer:
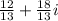
The expression is in a+bi form where,
a = 12/13
b = 18/13
================================================
Work Shown:
Multiply top and bottom by 3-2i, which is the conjugate of the original denominator. This will make the denominator go from a nonreal complex number to a purely real number.

The last expression is in a+bi form where a = 12/13 and b = 18/13
Keep in mind that
 has both sides square to
has both sides square to
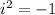 . Also, I'm using the difference of squares rule to go from
. Also, I'm using the difference of squares rule to go from
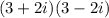 to
to
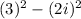 .
.