Question

Find the indicated angle or side. Give an exact answer.
Find the exact length of side a.

Answer 1

If you follow c²=a²+b² you can find your solution or you can do it with the cosinus rule/ sinus rule. But i don't see the side a remarked in your picture so i don't know which one you want to calculate.

Explanation:

Answer 2

The correct option is c.

The exact length of side a is 4 units.

To find the length of side a in the given right-angled triangle, we can use trigonometric ratios. Here are the steps:

1. Identify the known sides and angles: In the triangle, we know the length of side BC (which is 2 units) and angle ACB (which is 60 degrees). We need to find the length of side
`\( AB \) (side \( a \))`.

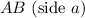2. Choose the appropriate trigonometric ratio: Since we have the adjacent side BC and we need to find the hypotenuse
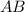`\( AB \)`, we can use the cosine ratio, which is given by:

`\[ \cos(\theta) = \frac{\text{Adjacent side}}{\text{Hypotenuse}} \]`

3. Apply the cosine ratio: Substituting the given values:

`\[ \cos(60^\circ) = (2)/(a) \]`

4. Calculate the value of
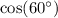`\( \cos(60^\circ) \)`: We know from trigonometry that
`\( \cos(60^\circ) = 0.5 \)`.

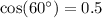5. Solve for a:

`\[ 0.5 = (2)/(a) \]`

6. Calculate a:

`\[ a = (2)/(0.5) \]`

`\[ a = 4 \]`

Therefore, the answer is 4 units.