- Let the breadth of rectangle be x.Thus, the length will be 2x.And we given – Perimeter is 72 meter.
⠀⠀⠀━━━━━━━━━━━━━━━━━━━━━━━━━━⠀⠀⠀⠀



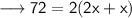

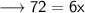

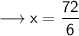

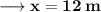
- Breadth of rectangle is 12 m.
We know that, value of x is '12'. Therefore, we'll substitute the value of x in given Length 2x to find out the Length. Therefore —
⠀

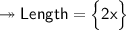

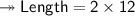


- Hence, length will be 24 m.

More To know :-
⠀
☀️
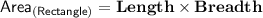
☀️
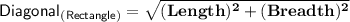
⠀⠀⠀━━━━━━━━━━━━━━━━━━━━━━━━━━⠀⠀⠀⠀