Question

Can someone help me with 6,7,8 please and if you can , can you explain it?

Answer 1

6) x = 3, y = -1 or (3, -1)

8) x = -1, y = ½ or (-1, ½)

Explanation:

Note:

I will only demonstrate problems 6 and 8 since the process of solving for the solution is practically similar for problems 6 and 7.

Given the following systems of linear equations with two variables:

Question 6

`\displaystyle\mathsf{\left \{{{Equation\:1:\:x\:+\:y=2} \atop {Equation\:2:\:2x\:-\:y=7}} \right. }`

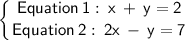
First, isolate y from Equation 1:

x + y = 2

x - x + y = -x + 2

y = -x + 2

Substitute the value of y in the previous step into Equation 2:

2x - (-x + 2) = 7

2x + x - 2 = 7

3x - 2 = 7

Add 2 to both sides:

3x - 2 + 2 = 7 + 2

3x = 9

Divide both sides by 3 to solve for x:

`\displaystyle\mathsf{(3x)/(3)\:=\:(9)/(3)}`

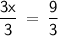
x = 3

Substitute the value of x into Equation 1 to solve for y:

x + y = 2

3 + y = 2

3 - 3 + y = 2 - 3

y = -1

Therefore, the solution to the given system is: x = 3, y = -1 or (3, -1).

Question 8:

`\displaystyle\mathsf{\left\{Equation\:1:\:3(6x\:-\:4y)\:=24} \atop{Equation\:2:\:3x\:-\:2y\:=4}} \right.}`

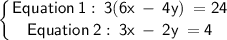
For Equation 2, divide both sides by -3:

`\displaystyle\mathsf{(-3(6x-4y))/(-3)=(24)/(-3) }`

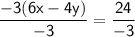
6x - 4y = -8

Add 6x to both sides:

6x + 6x - 4y = 6x - 8

- 4y = 6x - 8

Divide both sides by -4 to isolate y:

`\displaystyle\mathsf{(-4y)/(-4)=(6x\:-\:8)/(-4) }`

`\displaystyle\mathsf{y=-(3)/(2)+2}`

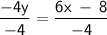
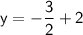
Substitute the value of y from the previous step into Equation 2:

3x - 2y = -4

`\displaystyle\mathsf{3x\:-\:2\Big(-(3)/(2)+2\Big)\:=-4}`

3x + 3 - 4 = -4

3x - 1 = -4

3x - 1 + 1 = -4 + 1

3x = -3

Divide both sides by 3 to solve for x:

`\displaystyle\mathsf{(3x)/(3)=(-3)/(3)}`

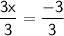
x = -1

Substitute the value of x into Equation 2 to solve for y:

3x - 2y = -4

3(-1) - 2y = -4

-3 - 2y = -4

Add 3 to both sides:

-3 + 3 - 2y = -4 + 3

-2y = -1

Divide both sides by -2 to isolate y:

`\displaystyle\mathsf{(-2y)/(-2)=(-1)/(-2)}`

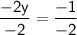
y = ½

Therefore, the solution to the given system is: x = -1, y = ½ or (-1, ½).