Problem 1
Answer: Choice C) -511
---------------------------------------
Work Shown:
- a1 = 9 = first term
- d = -7 = common difference
We decrease by 7 each time we need a new term
an = nth term
an = a1+d(n-1)
an = 9+(-7)(n-1)
an = 9-7n+7
an = -7n+16
a14 = -7*14+16
a14 = -82
Sn = sum of the first n terms of an arithmetic sequence
Sn = (n/2)*(a1+an)
S14 = (14/2)*(9+(-82))
S14 = -511
================================================
Problem 2
Answer: Choice C)
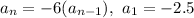
--------------------------------------
Step-by-step explanation:
The nth term of a geometric sequence is a*r^(n-1)
- a = first term
- r = common ratio
We're given that
- a2 = 15 = second term
- a5 = -3240 = fifth term
Those two facts lead us to these two equations
Divide the second equation over the first equation
The left hand sides would divide to r^3
The right hand sides divide to -216
Solving r^3 = -216 leads to r = -6
This leads to...
a*r = 15
a*(-6) = 15
a = 15/(-6)
a = -2.5
This points us at choice C as the answer. Choice C says that the nth term is found by multiplying the previous term by -6, which is tied directly to the common ratio.