For the integral ∫asin(x)dx, use integration by parts ∫udv=uv−∫vdu.
Let u=asin(x) and dv=dx.
Then du=(asin(x))′dx=
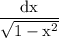 and v=∫1dx=x
and v=∫1dx=x
So,
![\rm{\int{\operatorname{asin}{\left(x \right)} d x}}=\color{h}{\left(\operatorname{asin}{\left(x \right)} \cdot x-\int{x \cdot \frac{1}{\sqrt{1 - x^(2)}} d x}\right)}=\color{h}{\left(x \operatorname{asin}{\left(x \right)} - \int{\frac{x}{\sqrt{1 - x^(2)}} d x}\right)} \\]()
Let u=1−x2.
Then du=(1−x2)′dx=−2xdx and we have that xdx=−du/2.
The integral can be rewritten as
![\rm x \operatorname{asin}{\left(x \right)} - \color{g}{\int{\frac{x}{\sqrt{1 - x^(2)}} d x}} = x \operatorname{asin}{\left(x \right)} - \color{j}{\int{\left(- (1)/(2 √(u))\right)d u}} \\]()
Apply the constant multiple rule ∫cf(u)du=c∫f(u)du with c=-1/2 and f(u)=
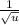
![\rm x \operatorname{asin}{\left(x \right)} - \color{h}{\int{\left(- (1)/(2 √(u))\right)d u}} = x \operatorname{asin}{\left(x \right)} - \color{h}{\left(- \frac{\int{(1)/(√(u)) d u}}{2}\right)} \\]()
Apply the power rule
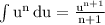
with n=−1/2
![\rm x \operatorname{asin}{\left(x \right)} + \frac{\color{h}{\int{(1)/(√(u)) d u}}}{2}=x \operatorname{asin}{\left(x \right)} + \frac{\color{j}{\int{u^{- (1)/(2)} d u}}}{2}=x \operatorname{asin}{\left(x \right)} + \frac{\color{j}{\frac{u^{- (1)/(2) + 1}}{- (1)/(2) + 1}}}{2}=x \operatorname{asin}{\left(x \right)} + \frac{\color{j}{\left(2 u^{(1)/(2)}\right)}}{2}=x \operatorname{asin}{\left(x \right)} + \frac{\color{h}{\left(2 √(u)\right)}}{2} \\]()
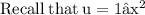
![\rm x \operatorname{asin}{\left(x \right)} + \sqrt{\color{re}{u}} = x \operatorname{asin}{\left(x \right)} + \sqrt{\color{rd}{\left(1 - x^(2)\right)}} \\]()
Therefore,
![\rm\int{\operatorname{asin}{\left(x \right)} d x} = x \operatorname{asin}{\left(x \right)} + \sqrt{1 - x^(2)}+C \\]()