Answer:
16 tons, $9108
Explanation:
Let's set up our equation. I can already tell you that each of these are linear equations. A linear equation can be set up with y=mx+b (slope-intercept form).
This will be helpful since the problem is telling you the slope (m) and the constant (b). b is also known as the y-intercept.
The problem says the first company charges $7500 to rent trucks plus an additional fee of $100.50 for each ton of sugar.
When you see the words, for each, per, for every, etc; that will be your slope (m). The $7500 is our constant (b).
Now to construct our equation for the first company it will be this:
y=100.50x+7500
Apply the same thing for the second company, $6296 to rent trucks plus $175.75 for each ton of sugar:
y = 175.75x+6296
Now that you have the equations of both companies, the problem is asking you for two things:
- When will the companies have the same cost (x)
- What the cost will be when the cost is the same (y)
But to this, we need some formula right? You could do this via looking on a graph but it may be hard if you don't have the appropriate technology. However, we just so happen to remember that we can set these equations together to find what value of x will both equations be the same.
Set the equations equal to each other:
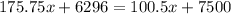
And solve for x
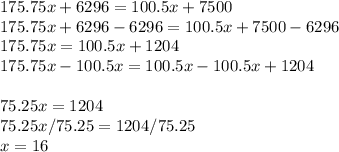
When using this equation, this means that when x is 16, both equations will equal each other. We have solved the first question.
Now to solve for y, we replace x with the number we found, 16. You can choose any equation since they both will be the same at x = 16.
y=175.75(16) + 6296 = 9108
The cost will be $9108 when both companies cost the same amount.