Question

Write an EQUATION with an undefined slope:

Answer 1

Example of an equation with an undefined slope: x = 2

Explanation:

Definitions

The standard form of linear equations with an undefined slope is x = a, whose graph represents a vertical line. The value of a in the standard form is the x-intercept, (a, 0).

The slope is the ratio of the vertical change in y-values to the horizontal change in x-values.

`\displaystyle\mathsf{Slope(m) =\:(\triangle y)/(\triangle x)\:=(y_2 - y_1)/(x_2 - x_1)}`

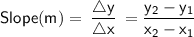
The slope of a vertical line is undefined because if we were to solve its slope, the denominator will be zero. As we know, division by zero is an undefined operation.

Example:

For example, suppose that we have the following points (2, 5) (2, 10).

Let (x₁, y₁) = (2, 5)

(x₂, y₂) = (2, 10)

Substitute these values into the slope formula:

`\displaystyle\mathsf{Slope(m) =\:(\triangle y)/(\triangle x)\:=(y_2 - y_1)/(x_2 - x_1)\:=\:(10\:-\:5)/(2\:-\:2)\:=(5)/(0)}`

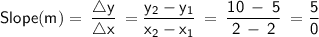
Dividing the numerator, 5, by the denominator, 0, will have an undefined quotient.

Thus, the equation of the vertical line will be: x = 2, where a = 2.