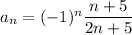The numerators in each term are consecutive integers ≥ 6. If n = 1 refers to the first term, then the numerator of the n-th term would be n + 5.
The denominators are consecutive odd integers ≥ 7. Odd numbers take the form 2k - 1, where k is any integer, and 2k - 1 = 7 when k = 4. But we want our sequence to start at n = 1, so we replace k here with n + 3. Then the denominator of the n-th term would be 2 (n + 3) - 1, or 2n + 5.
The odd-indexed terms are negative, while the even-indexed terms are positive. We can account for the sign of the term by multiplying by (-1)ⁿ.
Taking everything together, it follows that the n-th term in the sequence is