- A right isosceles triangle has legs that are each 10 mm.
- Here, base (b) = 10 mm
- Height (h) = 10 mm
- Let the length of the hypotenuse be x.
- Therefore, in the right triangle
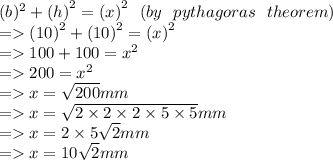
- So, the length of the hypotenuse is 10√2 mm.
Answer:
10√2 mm.
Hope you could get an idea from here.
Doubt clarification - use comment section.