First, look for the zeroes of the integrand in the interval [0, 6] :
x² - 6x + 8 = (x - 4) (x - 2) = 0 ⇒ x = 2 and x = 4
Next, split up [0, 6] into sub-intervals starting at the zeroes we found. Then check the sign of x² - 6x + 8 for some test points in each sub-interval.
• For x in (0, 2), take x = 1. Then
x² - 6x + 8 = 1² - 6•1 + 8 = 3 > 0
so x² - 6x + 8 > 0 over this sub-interval.
• For x in (2, 4), take x = 3. Then
x² - 6x + 8 = 3² - 6•3 + 8 = -1 < 0
so x² - 6x + 8 < 0 over this sub-interval.
• For x in (4, 6), take x = 5. Then
x² - 6x + 8 = 5² - 6•5 + 8 = 3 > 0
so x² - 6x + 8 > 0 over this sub-interval.
Next, recall the definition of absolute value:

Then from our previous analysis, this definition tells us that
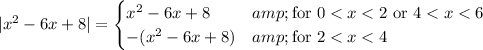
So, in the integral, we have

Then
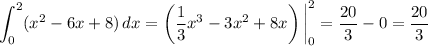
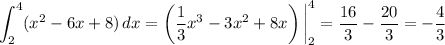
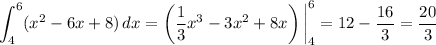
and the overall integral would be
20/3 - (-4/3) + 20/3 = 44/3