Question

Find the 62nd term of the arithmetic sequence
15, 13, 11, ...

Answer 1

`a_(62)=-107`

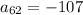
Explanation:

This is an arithmetic sequence:

`a_n=a_1+(n-1)d`

where d is the common difference and n is the index of any given term.

The common difference of the given sequence is -2:

`13-15=-2\\11-13=-2`

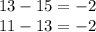
Using the first term and the common difference, you can write the equation for this sequence:

`a_n=15+(n-1)(-2)`

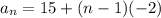
And using that equation, you can find the 62nd term:

`a_(62)=15+(62-1)(-2)\\a_(62)=15+(61)(-2)\\a_(62)=15-122\\a_(62)=-107`