Answer:
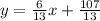
Explanation:
(x1, y1) = (-7, 5)
(x2, y2) = (6, 11)
The firs thing to do is fine the slope. That is the distance between the y-coordinates divided by the distance between the x-coordinates:

I marked the points above as points 1 and 2, so you can plug those numbers into the formula:
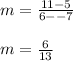
That fraction can't be simplified any further, so the slope of this line is 6/13. The next thing to do is to find the y-intercept.

Plug the slope and any point of your choice into the equation. I'll use point b:

Now, solve for b:
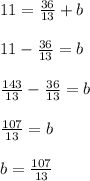
They're far from clean, but those are the correct slope and y-intercept. Using those, the equation for this line is:
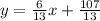
You can confirm that this is the correct equation by checking it with one of the points. Plug in one of the known values of x and make sure it gives the correct value of y:
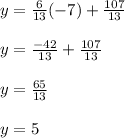
That works out.