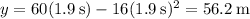56.2 m
Explanation:
We can solve for the maximum height by calculating the derivative of y with respect to time and then equating it to zero, i.e.,
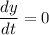
then solve for the time t that satisfies the equation above. The expression for the height y is
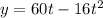
Taking the derivative of this expression, we get

This means that at t = 1.9 s, the ball would have reached its maximum height. To determine this height, use this value for t in the the equation for y to get