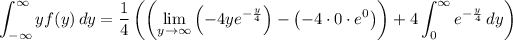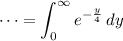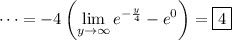Question

Hi need help for this maths question

Answer 1

a) If f(y) is a probability density function, then both f(y) ≥ 0 for all y in its support, and the integral of f(y) over its entire support should be 1. eˣ > 0 for all real x, so the first condition is met. We have

`\displaystyle \int_(-\infty)^\infty f(y) \, dy = \frac14 \int_0^\infty e^(-\frac y4) \, dy = -\left(\lim_(y\to\infty)e^(-\frac y4) - e^0\right) = \boxed{1}`

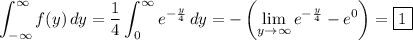
so both conditions are met and f(y) is indeed a PDF.

b) The probability P(Y > 4) is given by the integral,

`\displaystyle \int_(-\infty)^4 f(y) \, dy = \frac14 \int_0^4 e^(-\frac y4) \, dy = -\left(e^(-1) - e^0\right) = (e - 1)/(e) \approx \boxed{0.632}`

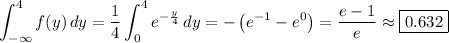
c) The mean is given by the integral,

`\displaystyle \int_(-\infty)^\infty y f(y) \, dy = \frac14 \int_0^\infty y e^(-\frac y4) \, dy`

Integrate by parts, with

`u = y \implies du = dy`

`dv = e^(-\frac y4) \, dy \implies v = -4 e^(-\frac y4)`

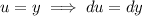
Then

`\displaystyle \int_(-\infty)^\infty y f(y) \, dy = \frac14 \left(\left(\lim_(y\to\infty)\left(-4y e^(-\frac y4)\right) - \left(-4\cdot0\cdot e^0\right)\right) + 4 \int_0^\infty e^(-\frac y4) \, dy\right)`

`\displaystyle \cdots = \int_0^\infty e^(-\frac y4) \, dy`

`\displaystyle \cdots = -4 \left(\lim_(y\to\infty) e^(-\frac y4) - e^0\right) = \boxed{4}`