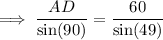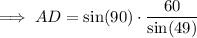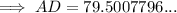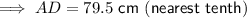Answer:
(a) BC = 91 cm
(b) ∠C = 33.4° (nearest tenth)
(c) AD = 79.5 cm (nearest tenth)
Explanation:
(a) Pythagoras' Theorem: a² + b² = c²
(where a and b are the legs, and c is the hypotenuse, of a right triangle)
Given:
- a = AB = 60 cm
- b = BC
- c = AC = 109 cm
⇒ 60² + BC² = 109²
⇒ 3600 + BC² = 11881
⇒ BC² = 11881 - 3600
⇒ BC² = 8281
⇒ BC = √(8281)
⇒ BC = 91 cm
(b) Sine rule to find an angle:
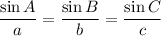
(where A, B and C are the angles, and a, b and c are the sides opposite the angles)
Given:
- ∠B = 90°
- b = AC = 109 cm
- c = AB = 60 cm

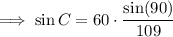
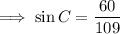
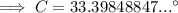

(c) Sine rule to find a side length:

(where A, B and C are the angles, and a, b and c are the sides opposite the angles)
Sum of interior angles of a triangle = 180°
Given:
- ∠B = 90°
- b = AD
- ∠D= 180° - 41° - 90° = 49°
- d = AB = 60 cm