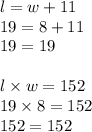Answer:
The dimensions of the lid are 8mm by 19mm.
w = 8
l = 19
Explanation:
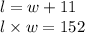
where l is length and w is width. This can be solved as a system of equations.
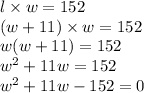
At this point, it gets a little tough. I might be unnecessarily overcomplicating things, but this is the only way I see to solve the problem.
=================== Skip down below if you don't care about factoring
You need to factor the newly created trinomial.
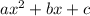
With a trinomial in this form, you need to find 2 numbers that add together to make b and multiply together to make ac.
Here, we need 2 numbers that add to 11 and multiply to -152. First, factor 152:
1, 152
2, 76
4, 38
8, 19
Then the reverse of all of those is true too, of course:
19, 8
38, 4
etc
In our case, we're looking for -152, so one of our factors will be negative. We're also looking for factors that add up to 11. Looking at these factors, you can see that 19 - 8 = 11, so our factors are 19 and -8.
Finally, you can use those to factor our trinomial. Split up the middle number (11w) into two:
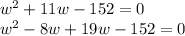
And now, you can factor by grouping:
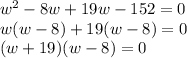
===================
Now that the number is factored, you can finally find w:
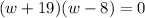
Here, you can see that the equation will be true when w = -19 or w = 8. Those are our solutions, but we can't have a negative distance, so it's just
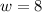
Going all the way back to the top, now you can use the width to find the length.
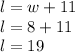
That one was much easier.
The dimensions of the lid are 8mm by 19mm.
Finally, check that with both of the original equations to make sure it's correct.