Question

60 points! Please answer fast and show your work... Thank you!

You would like to purchase the car in 2 years. How much money will you need to invest at a 3.3% interest rate compounded annually in order to have $9500 in 2 years? Use the compound interest formula A = P (1 + i)n. (Round final answer to the nearest cent, but otherwise don’t round any intermediate values)

Answer 1

`\bold{Formula: A = P(1 + (r)/(100))^((n))}`

Where

• A = Amount
• P = Principal
• R = Rate
• N = time compounded

`\bold{Solution : } \\ \\ \: \: \: \: \tt \: A = 9,500(1+(3.3\%)/(100))^((2)) \\ \: \: \: \: \: \: \tt \: A = 9,500(1+ 0.033)^((2)) \\ \tt \: A = 9,500(1.033)^((2)) \: \: \\ \tt \: A = 10,137.34 \qquad \: \: \:`

therefore,I need $10,137.34 if would like to purchase the car.

Answer 2

$ 8902.72

Explanation:

We would like to calculate the money which we need to invest at 3.3% rate compounded annually for two years . We know that ,

`\longrightarrow \boldsymbol{ A = P \bigg(1+(R)/(100)\bigg)^n }`

where the symbols have their usual meaning . So here ,

• Amount = $ 9500
• time = 2 years
• Rate = 3.3%
• P = The money we need to invest (?)

`\longrightarrow \$ 9500 = P \bigg( 1+(3.3)/(100)\bigg)^2\\`

Simplify RHS ,

`\longrightarrow \$ 9500 = P \bigg((100+3.3)/(100)\bigg)^2\\`

Simplify Nr . in RHS ,

`\longrightarrow \$ 9500 =P\bigg((103.3)/(100)\bigg)^2\\`

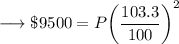
Isolate P ,

`\longrightarrow P = ( \$9500* 100* 100)/(103.3* 103.3)\\`

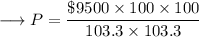
Simplify ,

`\longrightarrow \underline{\underline{\boldsymbol{ P = \$ 8902.72 }}}{}`

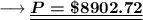
And we are done !