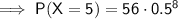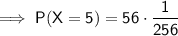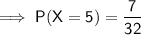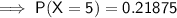Question

A coin is flipped 8 times. Find the probability of the event: Exactly 5 heads

a.0.625
b.0.03125
c.0.219
d.0.0039

Answer 1

c. 0.219

Explanation:

If the coin is fair, then the probability of flipping a head is 1/2 = 0.5

Therefore, we can model this as a binomial distribution:

X ~ B(n, p) where n is the number of events and p is the probability of success

Given:

• n = 8
• p = 0.5

X ~ B(8, 0.5)

Using a calculator:

P(X = 5) = 0.21875 = 0.219 (3 dp)

Using the formula:

`\sf P(X=x)=(n!)/((n-x)!x!)p^x(1-p)^(n-x)`

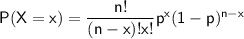
(where n is the number of events, x is the number of desired successes and p is the probability of success)

`\sf \implies P(X=5)=(8!)/((8-5)!5!)0.5^5(1-0.5)^(8-5)`

`\sf \implies P(X=5)=(8!)/(3!5!)0.5^50.5^3`

`\sf \implies P(X=5)=56 \cdot 0.5^8`

`\sf \implies P(X=5)=56 \cdot (1)/(256)`

`\sf \implies P(X=5)=(7)/(32)`

`\sf \implies P(X=5)=0.21875`