Let us consider a 30°-60°-90°△ABC right angled at B in which ∠C = 30⁰ and ∠A = 60⁰ with hypotenuse AC = 10√2 units.
Solution:-
In △ABC,
 sin ∠C =
sin ∠C =
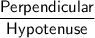
 sin ∠C =
sin ∠C =
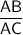
 sin 30⁰ =
sin 30⁰ =
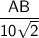

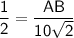

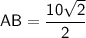

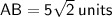

In △ABC,
 cos ∠C =
cos ∠C =
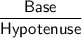
 cos ∠C =
cos ∠C =
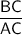
 cos 30⁰ =
cos 30⁰ =
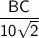

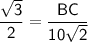

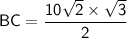

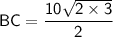

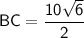

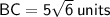
Thus , the length of other two sides of triangles are 5√2 and 5√6 units.