Answer:
- Perimeter of Traingle is 10 + 2√5

Step-by-step explanation:
Let,
- A = (1,4)
- B = (1,-2)
- C = (-3,-2)

To find the perimeter of the traingele with vertices of A (1,4), B(1, -2) and C(-3,-2). We have to first find the distance between each pair of points, which will give length of the sides.

Using distance formula,

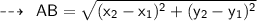
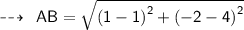
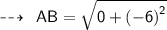
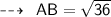

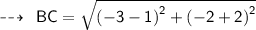
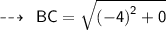
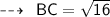
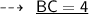
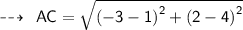
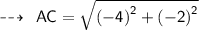
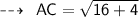
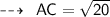
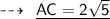

Now,

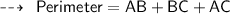
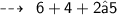


Hence,
- Perimeter of Traingle is 10 + 2√5