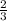Answer:
sinΘ =
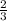
Explanation:
using the identity
sin²x + cos²x = 1 ( subtract cos²x from both sides )
sin²x = 1 - cos²x ( take square root of both sides )
sinx = ±
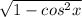
given
cosΘ = -
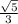 , then
, then
sinΘ = ±
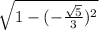
= ±
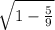
= ±
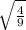
= ±
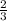
since Θ is in quadrant II where sinΘ > 0 , then
sinΘ =