If
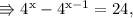
then (2x)^x equals
(a) 5√5
(b) √5
Note:-
Make sure you include all steps.
Proper explanation is mandatory .
Spams/irrelevant/wrong/copied answers will be deleted on the spot so don't waste your precious time here by spamming .
Instead provide good explanation and correct answer