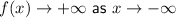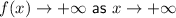Question

50 points hlep Explain how to graph a polynomial function in factored form. What do the factors mean in terms of the polynomial? Graph f(x)=(x−2)^2 (x+1) (x−4)

Answer 1

Given function:
`f(x)=(x-2)^2 (x+1) (x-4)`

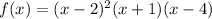
The factors give us the zeros (x-intercepts) of the graph.

To find the zeros, set the function to zero and solve for x:

`(x-2)^2 (x+1) (x-4)=0`

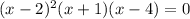
Therefore,

`(x-2)^2=0\implies x-2=0 \implies x=2`

`(x+1)=0\implies x=-1`

`(x-4)=0 \implies x=4`

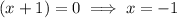
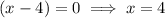
So the zeros are at (2, 0) (-1, 0) and (4, 0)

The multiplicity of a zero is the number of times the factor appears in the fully factored form of the polynomial, i.e. the exponent on the corresponding factor.

• 
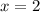  `x = 2` has a multiplicity of 2
• 
  `x=-1` has a multiplicity of 1
• 
  `x=4` has a multiplicity of 1

If the zero has an even multiplicity, the graph touches and bounces off the x-axis at that point.

If the zero has an odd multiplicity, the graph crosses the x-axis at that point.

To find the y-intercept, expand the function:

`f(x)=x^4-7x^3+12x^2+4x-16`

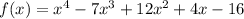
Set
`x = 0` and solve:

`f(0)=(0)^4-7(0)^3+12(0)^2+4(0)-16=-16`

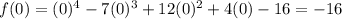
Therefore, the y-intercept is at (0, -16)

The end behavior of a polynomial function is the behavior of the graph of f(x) as x approaches positive infinity or negative infinity.

As the leading degree is 4 (even) and the leading coefficient is positive, the end behavior of the function is:

`f(x) \rightarrow + \infty \textsf{ as } x \rightarrow - \infty`

`f(x) \rightarrow + \infty \textsf{ as } x \rightarrow + \infty`