Answer:
y = -
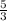 x - -
x - -

Explanation:
First, let's divide both sides by 5 to get the first equation into the form y = mx + b. We get y =
 x + 5. The m value,
x + 5. The m value,
 , is the slope and the b value, 5, is the y-intercept of this line.
, is the slope and the b value, 5, is the y-intercept of this line.
When a line is perpendicular to another line, the slopes must multiply to get -1. In other words, the slopes must be a negative reciprocal of each other. Since the slope of the original line is
 , we know that the slope of the line perpendicular to that is -
, we know that the slope of the line perpendicular to that is -
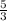 .
.
Then, since we know x, y, and m of the second equation, we can substitute those three values into the equation, y = mx + b, to find the y-intercept (b).
-1 = (-
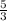 )(-4) + b
)(-4) + b
-1 =
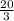 + b
+ b
b = -

After plugging in the values of m and b we calculated, we get the equation for the line perpendicular to the original line: y = -
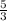 x -
x -
 .
.