Answer:
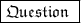
What is the degree of polynomial?
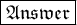
The degree of a polynomial is the highest of the degrees of the polynomial's monomials with non-zero coefficients.
Example:
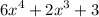
4x The Degree is 1 (a variable without an
exponent actually has an exponent of 1)
More Examples:
4x^ − x + 3 The Degree is 3 (largest exponent of x)
x^2 + 2x^5 − x The Degree is 5 (largest exponent of x)
z^2 − z + 3 The Degree is 2 (largest exponent of z)
A constant polynomials (P(x) = c) has no variables. Since there is no exponent to a variable, therefore the degree is 0.
3 is a polynomial of degree 0.