Question

A sector on a circle with a radius of 5 units has an area of 18.751 square units. What is

the measure of the central angle?

Answer 1

As Per Provided Information

Radius of sector 5 units

Area of sector 18.751 square units

we have been asked to determine the measure of the central angle .

Using Formulae

`\underline{ \boxed{\bf\pink{Area_((Sector)) \: = \cfrac{ \theta * \pi {r}^(2) }{360 {}^( \circ)}}}}`

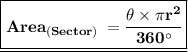
Substituting the given value and let's solve it

`\longrightarrow \sf \: 18.751 = \cfrac{ \theta * 3.14 * {5}^(2) }{360} \\ \\ \ \\ \longrightarrow \sf \: 18.751 * 360 = { \theta * 3.14 * 25} \\ \\ \\ \longrightarrow \sf \: 6750.36 \: = \theta \: * 78.5 \\ \\ \\ \longrightarrow \sf \theta \: = \: \cfrac{6750.36}{78.5} \\ \\ \\ \longrightarrow \sf \theta \: = \cancel\cfrac{6750.36}{78.5} \\ \\ \\ \longrightarrow \sf \theta \: = 85.99 {}^( \circ) \\ \\ \\ \longrightarrow \sf \theta \: = \: \approx \: 86 {}^( \circ)`

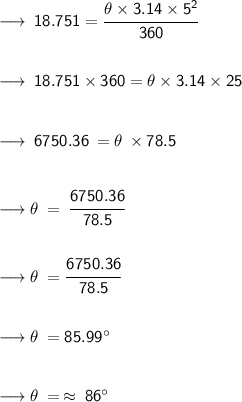
Therefore,

• Measure of central angle is 86°