Answer:
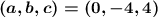
Explanation:
We would like to solve the following system of equations ,
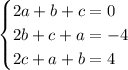
Firstly lets number the equations as ,
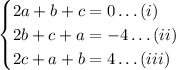
Again , we can rewrite the first equation as , equations as ;
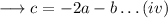
Now , substitute the value of equation (iv) in equation (ii) and (iii) .
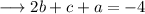
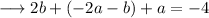
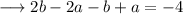
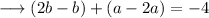
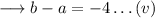
And ,
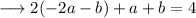
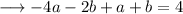
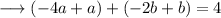
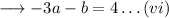
Now consider ,
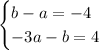
On adding these two equations, we have ;
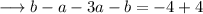
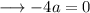
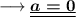
Now substitute this value in equation (v) ,
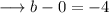
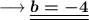
Finally substitute the values of a and b in equation (iv) , we have ;
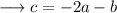
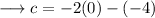
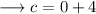
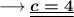
And we are done !