Answer:

Explanation:
The point-slope form of an equation for a line is y = mx + b (m is the slope; b is the y-intercept).
First, find the slope using the two given points.
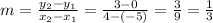
At this stage, you know the slope and need to find the y-intercept. Plug in one of the points (either one) into the equation. Let's use (-5, 0).
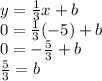
The equation for the line is
 .
.
You can check for errors by putting in the point you didn't use...
Check to make sure the point (4, 3) satisfies the equation.
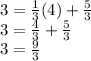 True!
True!