Answer:
k=100, n=3, 1.5625, 10
Explanation:
To find n and k, we can plug x and z in.
First we can try this for (1,100). We will get:
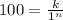
Since 1 to any power is 1, we can assume that the denominator is 1 and therefore k=100.
Armed with k=100, we can plug numbers into the second equation.
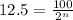
Moving
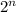 to the left side, we get:
to the left side, we get:

therefore we can solve and we see that n=3.
We can do the same for x=4, but since we have n, k, and x, we can plug these in to get z
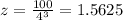
We will do the same as previous but instead plug in x

We isolate
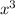 and get
and get
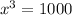
Therefore x=10