Question

Evaluate the difference quotient for the given function.

f(t) = g(t) h(t) , where g(t) = cos(t) and h(t) =sin(t)

Answer 1

Assuming you mean f(t) = g(t) × h(t), notice that

f(t) = g(t) × h(t) = cos(t) sin(t) = 1/2 sin(2t)

Then the difference quotient of f is

`\frac{\frac12 \sin(2(t+h)) - \frac12 \sin(2t)}h = (\sin(2t+2h) - \sin(2t))/(2h)`

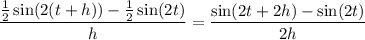
Recall the angle sum identity for sine:

sin(x + y) = sin(x) cos(y) + cos(x) sin(y)

Then we can write the difference quotient as

`(\sin(2t)\cos(2h) + \cos(2t)\sin(2h) - \sin(2t))/(2h)`

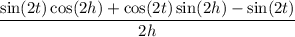
or

`\boxed{\sin(2t)(\cos(2h)-1)/(2h) + \cos(2t)(\sin(2h))/(2h)}`

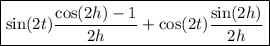
(As a bonus, notice that as h approaches 0, we have (cos(2h) - 1)/(2h) → 0 and sin(2h)/(2h) → 1, so we recover the derivative of f(t) as cos(2t).)