Question

How many solutions does this system have?

X + 2y = 0
10y = -5x
Choose the correct answer below.
No solution
O Exactly one solution
O Infinitely many solutions
Click to select your answer.

Answer 1

Infinitely many solutions

Explanation:

Given the system:

`\left \{ {{x+2y=0} \atop {10y=-5x}} \right.`

One way to do it is to use substitution. That means we want to isolate one of the variables in one equation so we can plug it into the other equation. We can isolate
`x` in the first equation by subtracting
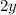`2y` from both sides.

`\left \{ {{x=-2y} \atop {10y=-5x}} \right.`

Now we know what
`x` is, so we can plug it into the bottom equation.

`10y=-5(-2y)`

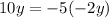
Then we simplify the right side:

`10y=10y`

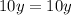
Then we divide both sides by 10:

`y=y`

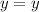
Since
`y` will ALWAYS be equivalent to itself, no matter what, we know that there are infinitely many solutions.

Answer 2

Infinitely many solutions