Question

Consider the following function.

f(x) = 1 + 5/x - 4/x2
(a) Find the vertical asymptote(s).
(b) Find the interval where the function is increasing.
Find the interval where the function is decreasing.
(c) Find the local maximum and minimum values.
(d) Find the interval where the function is concave up.
Find the interval where the function is concave down.
Find the inflection point.
(e) Use the information from parts (a)-(d) to sketch the graph of f.

Answer 1

See below

Explanation:

I assume the function is
`f(x)=1+(5)/(x)-(4)/(x^2)`

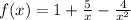
A) The vertical asymptotes are located where the denominator is equal to 0. Therefore,
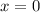`x=0` is the only vertical asymptote.

B) Set the first derivative equal to 0 and solve:

`f(x)=1+(5)/(x)-(4)/(x^2)`

`f'(x)=-(5)/(x^2)+(8)/(x^3)`

`0=-(5)/(x^2)+(8)/(x^3)`

`0=-5x+8`

`5x=8`

`x=(8)/(5)`

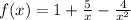
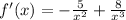
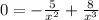
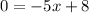
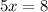
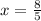
Now we test where the function is increasing and decreasing on each side. I will use 2 and 1 to test this:

`f'(2)=-(5)/(2^2)+(8)/(2^3)=-(5)/(4)+(8)/(8)=-(5)/(4)+1=-(1)/(4)`

`f'(1)=-(5)/(1^2)+(8)/(1^3)=-(5)/(1)+(8)/(1)=-5+8=3`

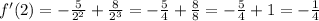
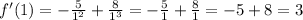
Therefore, the function increases on the interval
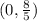`(0,(8)/(5))` and decreases on the interval
`(-\infty,0),((8)/(5),\infty)`.

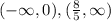C) Since we determined that the slope is 0 when
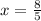`x=(8)/(5)` from the first derivative, plugging it into the original function tells us where the extrema are. Therefore,
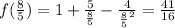`f((8)/(5))=1+(5)/((8)/(5))-(4)/((8)/(5)^2 )=(41)/(16)`, meaning there's an extreme at the point
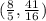`((8)/(5),(41)/(16))`, but is it a maximum or minimum? To answer that, we will plug in
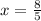`x=(8)/(5)` into the second derivative which is
`f''(x)=(10)/(x^3)-(24)/(x^4)`. If
`f''(x)>0`, then it's a minimum. If
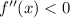`f''(x)<0`, then it's a maximum. If
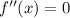`f''(x)=0`, the test fails. So,
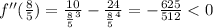`f''((8)/(5))=(10)/((8)/(5)^3)-(24)/((8)/(5)^4)=-(625)/(512)<0`, which means
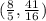`((8)/(5),(41)/(16))` is a local maximum.

D) Now set the second derivative equal to 0 and solve:

`f''(x)=(10)/(x^3)-(24)/(x^4)`

`0=(10)/(x^3)-(24)/(x^4)`

`0=10x-24`

`-10x=-24`

`x=(24)/(10)`

`x=(12)/(5)`

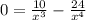
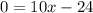
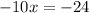
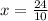
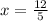
We then test where
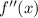`f''(x)` is negative or positive by plugging in test values. I will use -1 and 3 to test this:

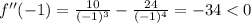`f''(-1)=(10)/((-1)^3)-(24)/((-1)^4)=-34<0`, so the function is concave down on the interval
`(-\infty,0)\cup(0,(12)/(5))`

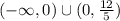
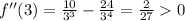`f''(3)=(10)/(3^3)-(24)/(3^4)=(2)/(27)>0`, so the function is concave up on the interval
`((12)/(5),\infty)`

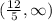
The inflection point is where concavity changes, which can be determined by plugging in
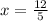`x=(12)/(5)` into the original function, which would be
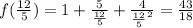`f((12)/(5))=1+(5)/((12)/(5))+(4)/((12)/(5)^2 )=(43)/(18)`, or
`((12)/(5),(43)/(18))`.

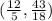E) See attached graph