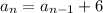Answer:
4) a₁₅ = 128
5) B.
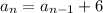
Explanation:
4)
This is an arithmetic sequence, where all terms have a common difference:
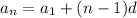
Here, the common difference is 9.
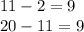
Use that to write the equation and solve for a₁₅:
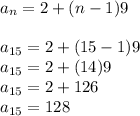
5)
This is also an arithmetic sequence, but it is a recursive arithmetic sequence in the form of:
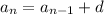
This simply states that each term is d more than the term before it.
Here, the common difference is 6:
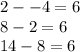
And the equation for this is B.