Question

Write each number in scientific notation. Show your work/explain.

A. 14,700
B. 0.00083
C. 760,000,000
D. 0.038
E. 0.38
F. 3.8
G. 3,800,000,000,000
H. 0.0000000009

Answer 1

Answer:
`1.47*10^4`

`8.3*10^(-4)`

`7.6*10^8`

`3.8*10^(-2)`

`3.8*10^(-1)`

`3.8*10^0`

`3.8*10^(12)`

`9.0*10^(-10)`

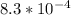
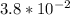
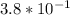
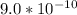
Explanation:

Scientific notation is a way of expressing numbers that are too large or too small.

To figure out the power of 10, think "how many places do I move the decimal point?"

1. When the number is 10 or greater, the decimal point has to move to the left, and the power of 10 is positive.

2. When the number is smaller than 1, the decimal point has to move to the right, so the power of 10 is negative.