Answer:
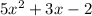
This answer is correct because I simplified using like terms.
Explanation:
Subtracting Polynomials
They key to subtract, multiply, add, and divide polynomials is by using like terms. Like terms are values with the same bases. For example :
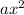 and
and
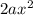 are like terms because they have the base
are like terms because they have the base
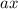
Step 1: Move like terms together
First, let's remove all parenthesis:
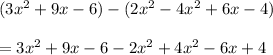
Now let's move all like terms together:
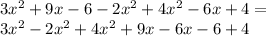
Step 2: Simplify
Now we can add and subtract the like terms like we do in any other problem
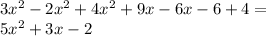
Step 3: Explaining your answer
Just say: "This answer is correct because I simplified using like terms"
-Chetan K