Answer:
Length of the shadow = 20.5 cm
Explanation:
Given the 32-meter height of a tall building, and its casted shadow of 38 meters, we can find the unknown length of the shadow by using the Pythagorean Theorem.
Definition:
The Pythagorean Theorem states that the squared length of the hypotenuse of a right triangle is equal to the sum of the squared lengths of the legs.
The algebraic representation of the Pythagorean Theorem is:
c² (hypotenuse) = a² (leg₁) + b² (leg₂)
Solution
To solve for the given problem:
Let c = 38 m (distance from the top of the building to the tip of the shadow)
a = unknown length of the shadow
b = 32m (height of the building)
Since we have to solve for the value of a (unknown length of the shadow), we must algebraically solve for a:
c² = a² + b²
Subtract b² from both sides:
c² - b² = a² + b² - b²
a² = c² - b²
Substitute the given values into the formula for solving a :
a² = c² - b²
a² = (38)² - (32)²
a² = 1444 - 1024
a² = 1444 - 1024
Next, take the square root of both sides to solve for a:
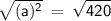
a = 20.49 or 20.5 cm
Therefore, the length of the shadow is 20.5 cm.